Why Can't We See The Flag On The Moon?
Return to my Astronomy page.
A common question asked at Star Parties, workshops, or other gatherings where Astronomy is discussed is:
Why can't we see the flag that the Apollo Astronauts left on the moon?
The answer is some basic Wakefield High School mathematics* as follows:
A. Lets assume that:
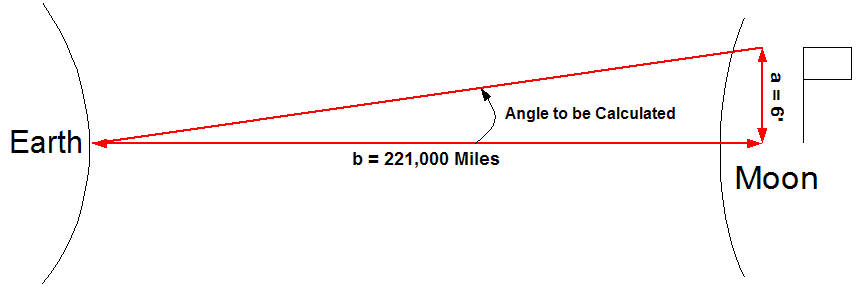
- The height of the flag (a) pole in ft. = 6
- The average distance to the Moon (approx) in miles = 221,000
- Which means that the distance to the Moon (approx) in feet (b) = 1,166,880,000
B. Given the above:
- The tangent (t) of the above in radians [tan(a/b)] = 0.0000000051, in radians
- Converted to Degrees [180*(t/pi)] = 0.000000295 degrees
- This means that a telescope would have to be able to resolve an angle of 2.95 x 10-07 degrees to see the flag left on the moon.
C. That means:
| Since one Arc Degree (1/360 of a circle) = | 1.000000000 Deg. |
| And one Arc Minute (1/60 of a degree) = | 0.016666667 Deg. |
| And one Arc Second (1/60 of an arc-minute) = | 0.000277778 Deg. |
| We can calculate that: | |
| The Angle to be resolved is: | 0.000000295 Deg. |
| And the Angle to be resolved in Arc Seconds is: | 0.001060596 |
So, to see the flag, a telescope must be able to resolve an angle of about 1/1000th of an arc second.
*The formulas in bold above can be used in most spreadsheets
"So how big of a telescope would that require?", you ask.
The Dawes limit calculates how close two objects can be and still be resolved by a telescope.
The formula is: Resolution (in arc seconds) = 4.56/Diameter.
So, to determine the required diameter, the formula is: D = 4.56/Resolution(arc seconds)
Doing the math, that is 4.56/.001060596 arc seconds, to see the flag a telescope would require a mirror 4,299.47 inches wide! That is 358.29 Feet!
A super-telescope THAT big would have to be in orbit, to eliminate the turbulence of the earth's atmosphere.
So, what distances can we see on the moon?
| Actual distances to the moon based on Rukl's Atlas of the Moon: | ||
|---|---|---|
| Kilometers | Miles | |
| Closest (perogee) | 356,400 | 221,457 |
| Average | 384,401 | 238,856 |
| Farthest (apogee)> | 406,700 | 252,712 |
| Lunar Diameter | 3476 | 2159.89 |
| The Moon's Angular Diameter at perogee (when it is closest to the earth) = | 33' 28.8" (33 min. 28.8 sec.) |
| Lunar Diameter in feet = | 11,404,199.48 |
| Total Angular diameter in Arc Seconds = | 2008.80 |
| Lunar Surface per Arc Second = | 5677.12 (ft.) |
| For a 10" telescope, Dawes Limit is 4.56/10 or | 0.456000 Arc-Seconds |
| So, the resolvable Distance with a 10" telescope is (5677.12)/(.456), or: | 2588.77 ft. |
| Our super-telescope distance resolved at .00106 Arc Seconds is: | 6.02 ft. |
Note: The Hubble Space Telescope can resolve .005 Arc Seconds, or about 280 Feet
(See Sky & Telescope 10/2004 pg 130)
If you want more information, e-mail the author at: |
 |